今天我們要來學習線性組合與 Span

什麼是線性組合

線性組合非常的簡單這邊就快速講過，就是當我們有一組向量v1,v2,...,vk，線性組合就是把它們乘上一個數（可以是正的、負的、零的小數或整數）然後加起來。例如：

v1 = (1,0)，v2 = (0,1)
那 3v1+2v2 = (3,0) + (0,2) = (3,2)

什麼是Span?

首先我們來看一組題目

S={(1,2,3),(2,4,6),(1,1,0)}⊂R3

首先我們來看看有沒有明顯的相依。這邊可以看到(1,2,3),(2,4,6)很明顯兩者為相依，因為 2(1,2,3) = (2,4,6)

接著我們可以看到有沒有常數使得(1,1,0)=c(1,2,3)？可以看到這兩個向量並沒有任何的相依性。也就是獨立的。到著我們認知到了幾個事情：

(1,2,3),(2,4,6)兩者為相依，因為2(1,2,3) = (2,4,6)
(1,1,0),(1,2,3)兩者為獨立，因為沒有常數使得(1,1,0)=c(1,2,3)

那這時候我們基於上述內容來找出 dim(span(S))，前面提到因為我們發現(1,2,3),(2,4,6)兩者為相依所以呢在向量空間中可以發現兩者是在同一條線上。而(1,1,0),(1,2,3)兩者為獨立因此在向量空間中會存在兩條線如下圖：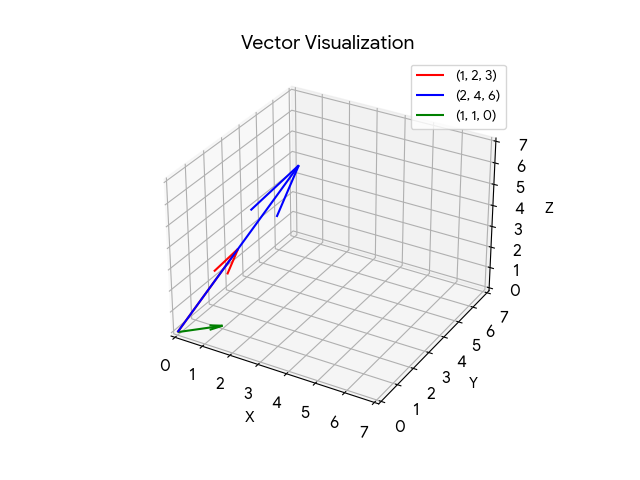

也就是說一組向量的 Span，就代表著所有向量的各種組合。像是如果只有一個非零向量v，Span 就是通過原點、沿著 v 的直線。那如果有兩個向量且不共線，Span 就是一個平面（通過原點），如下圖：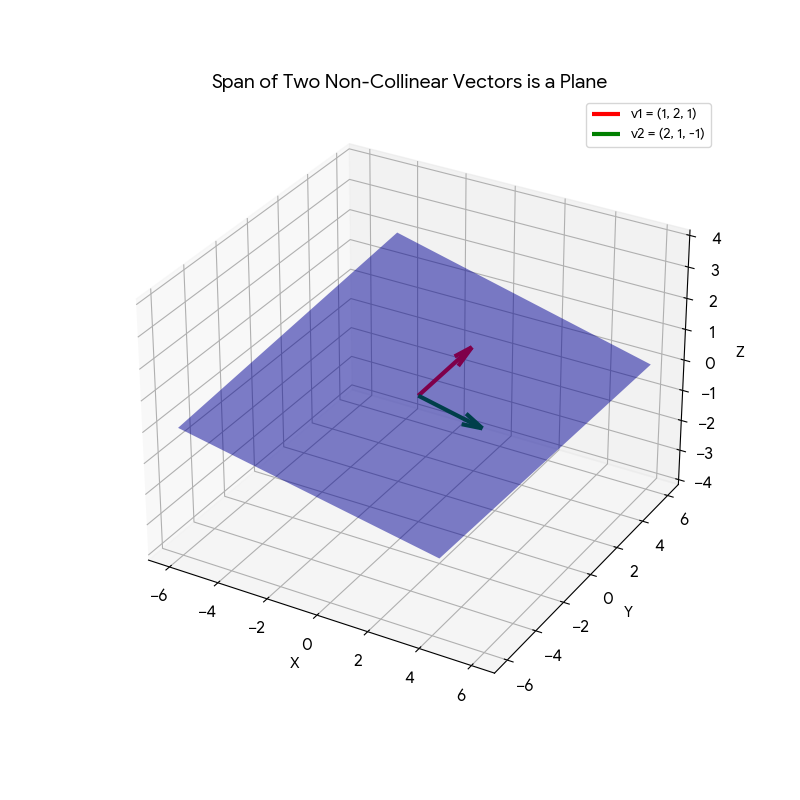

接著再進階一點，如果有三個向量而且足夠「分散」，Span 可能是整個三維空間。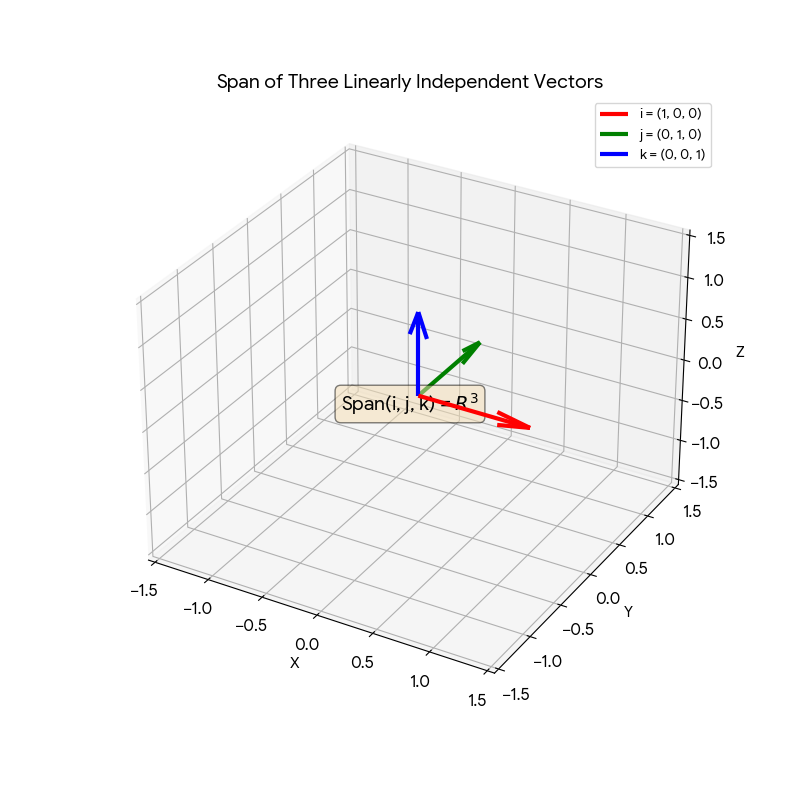

那我們來出個小練習給大家，今天有兩個向量分別是 v1=(2,1), v2=(4,2) 請問他們的Span 會是：（a)一條直線 （b)一個平面 （c)還是整個R＾2？

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃
ANS：可以看到 v1 = 2v2，因此兩者為線性組合這表示它們其實在同一條直線上，沒有「新的方向」。答案是 a ～

在資料科學中的用處？

其實這個名詞在資料科學中還蠻常見的～只是我們通常都稱作「特徵空間」(feature space) 或「向量空間」(vector space)。

像是在機器學習中，我們的資料點（樣本）其實就是向量。而這些向量的Span 表示：
用現有特徵可以線性組合生成的所有可能資料點的空間範圍。像是如果類別的向量分佈在不同 Span 之間。線性模型（如邏輯迴歸、線性 SVM）就有機會用一條（或超平面）來分開它們。那如果如果不同類別的資料都落在同一個小 Span 內，就可能需要非線性方法。如下圖：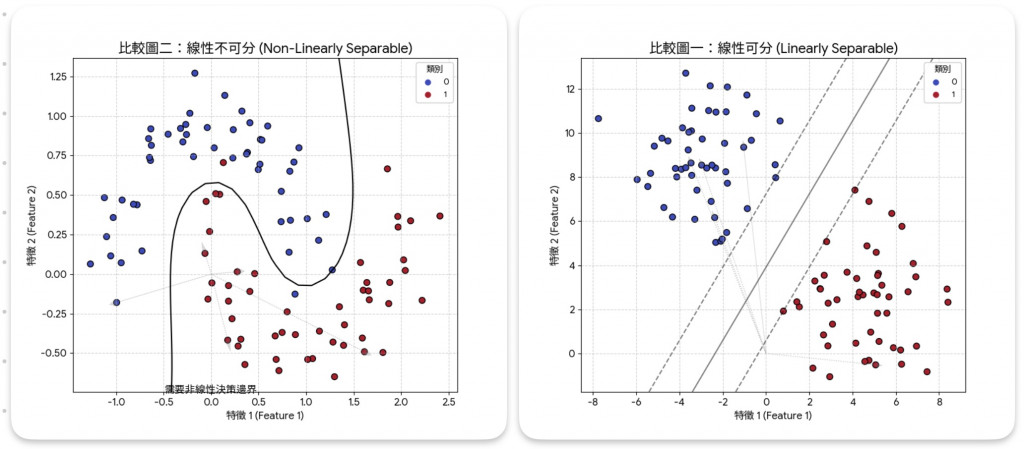

來用gpt最喜歡的結語，總而言之呢！Span 在資料科學中就是「你的特徵能覆蓋的向量空間」。